A Information to Customized Loss Capabilities and Calibration Metrics

Evaluating Deep Studying fashions is a necessary a part of mannequin lifecycle administration. Whereas conventional fashions have excelled at offering fast benchmarks for mannequin efficiency, they usually fail to seize the nuanced targets of real-world functions. As an illustration, a fraud detection system would possibly prioritize minimizing false negatives over false positives, whereas a medical analysis mannequin would possibly worth recall greater than precision. In such situations, relying solely on standard metrics can result in suboptimal mannequin habits. That is the place customized loss features and tailor-made analysis metrics come into play.

Typical Deep Studying Fashions Analysis

The standard measures to judge classification embrace Accuracy, Recall, F1-score, and so forth. Cross-entropy loss is the popular loss perform to make use of for classification. These typical measures of classification consider solely whether or not predictions have been right or not, ignoring uncertainty.

A mannequin can have excessive accuracy however poor chance estimates. Trendy deep networks are overconfident and return possibilities of ~0 or ~1 even when they’re improper.

Learn extra: Typical mannequin analysis metrics

The Downside

Guo et al. present {that a} extremely correct deep mannequin can nonetheless be poorly calibrated. Likewise, a mannequin might need a excessive F1 rating however nonetheless could possibly be miscalibrated in its uncertainty estimates. Optimizing goal features like accuracy or log-loss may produce miscalibrated possibilities, since conventional analysis metrics don’t assess whether or not the mannequin’s confidence matches actuality. As an illustration, a pneumonia detection AI would possibly output 99.9% chance based mostly on patterns that additionally happen in innocent situations, resulting in overconfidence. Calibration strategies like temperature scaling alter these scores so that they higher replicate true likelihoods.

What Are Customized Loss Capabilities?

A customized loss or goal perform is any coaching loss perform (apart from commonplace losses like cross-entropy and MSE) that you just invent to specific particular targets. You would possibly develop one when a extra generic loss doesn’t meet your corporation necessities. 

As an illustration, you might use a loss that penalizes false negatives, missed fraud, greater than false positives. This allows you to deal with uneven penalties or targets, like maximizing F1 as a substitute of simply accuracy. A loss is solely a clean mathematical method that compares predictions with labels, so you possibly can design any method that intently mimics the metric or value you need.

Why construct a Customized Loss Operate?

Generally the default loss under-trains on essential circumstances (e.g., uncommon lessons) or doesn’t replicate your utility. Customized losses provide the capacity to:

• Align with enterprise logic: e.g., penalize lacking a illness 5× greater than a false alarm.
• Deal with imbalance: downweight the bulk class, or give attention to the minority.
• Encode area heuristics: e.g., require predictions to respect monotonicity or ordering.
• Optimize for particular metrics: approximate F1/precision/recall, or domain-specific ROI.

How you can Implement a Customized Loss Operate?

On this part, we’ll implement a customized loss with PyTorch utilizing the nn.Module perform. The next are its key factors:

• Differentiability: Be certain that the loss perform is differentiable for the mannequin outputs.
• Numerical Stability: Use log-sum-exp or steady features in PyTorch (F.log_softmax, F.cross_entropy, and so on.). For instance, one can write Focal Loss by utilizing F.cross_entropy (containing softmax and log) in the identical approach, however then multiplying by (1−𝑝𝑡)𝛾. This technique avoids needing to compute the possibilities in a separate softmax, which may underflow.
• Code Instance: To display the concept, right here is how one would outline a customized Focal Loss in PyTorch:

import torch

import torch.nn as nn

import torch.nn.practical as F

class FocalLoss(nn.Module):

   def __init__(self, gamma=2.0, weight=None):

       tremendous(FocalLoss, self).__init__()

       self.gamma = gamma

       self.weight = weight  # weight tensor for lessons (non-obligatory)

   def ahead(self, logits, targets):

       # Compute commonplace cross entropy loss per-sample

       ce_loss = F.cross_entropy(logits, targets, weight=self.weight, discount='none')

       p_t = torch.exp(-ce_loss)          # The mannequin's estimated chance for true class

       loss = ((1 - p_t) ** self.gamma) * ce_loss

       return loss.imply()

Right here, γ tunes how a lot focus we would like on the arduous examples. The upper γ=extra focus, and this suggests that weight can deal with class imbalance.

We used Focal loss because the loss perform because it’s designed to deal with class imbalance in object detection and different machine studying duties, notably when coping with a lot of simply categorized examples, e.g., background in object detection. This makes it appropriate for our job. 

Why Mannequin Calibration Issues?

Calibration describes how nicely predicted possibilities correspond to real-world frequencies. A mannequin is well-calibrated if amongst all of the cases to which it assigns chance p to the optimistic class, about p fraction are optimistic. In different phrases, “confidence = accuracy”. As an illustration, if a mannequin predicts 0.8 on 100 check circumstances, we might anticipate about 80 to be right. Calibration is essential when utilizing possibilities for a call (e.g., threat scoring; cost-benefit evaluation). Formally, which means for a classifier with a chance output 𝑝^, calibration is:

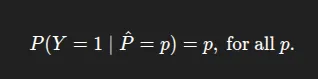
Calibration Errors

Calibration errors fall into two classes:

1. Overconfidence: Means the mannequin’s predicted possibilities are systematically greater than true possibilities (e.g., predicts 90%, however is correct 80% of the time). Deep neural networks are usually overconfident, particularly when overparameterized. Overconfident fashions could be harmful; they usually make sturdy predictions and may mislead us when misclassifying.
2. Underconfidence: Underconfidence is much less frequent in deep nets. That is the other of overconfidence, when the mannequin’s confidence is simply too low (e.g., predicts 60%, however is correct 80% of the time). Whereas underconfidence usually locations the mannequin in a safer place when predicting, it might look uncertain and thus much less helpful.

In apply, fashionable DNNs are usually overconfident. Guo et al. discovered that newer deep nets with batch norm, deeper layers, and so on., had spiky posterior distributions with very excessive chance on one class, even whereas misclassifying. After we make these miscalibrations, it’s crucial to comprehend them so we are able to make dependable predictions.

Metrics for Calibration

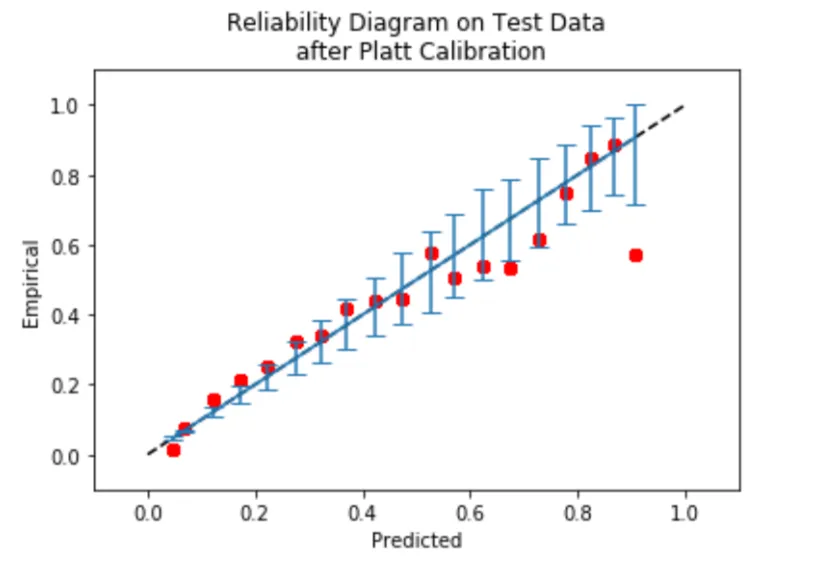
• Reliability Diagram: Calibration Curve Generally known as a reliability diagram, this additionally casts the anticipated successes into bins based mostly on the prediction’s confidence rating. For every bin, it plots the proportion of positives (y-axis) vs. the imply predicted chance on the x-axis.

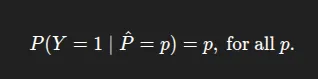
• Anticipated Calibration Error (ECE): It summarizes absolutely the distinction between accuracy and confidence, weighted by the scale of the bin. Formally, the place acc(b) and conf(b) are the accuracy and imply confidence in bin dimension. As a reminder, decrease values of ECE are higher (0=completely calibrated). ECE is a measure of common miscalibration. 

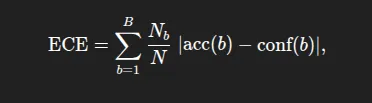
• Most Calibration Error (MCE): The most important hole over all bins:

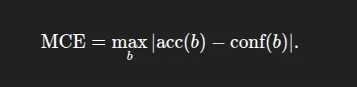
• Brier Rating: Brier rating is the imply squared error between the anticipated chance and the precise end result, which is both 0 or 1. It’s a correct scoring rule and captures each calibration and accuracy. Nevertheless, a smaller Brier rating doesn’t imply the predictions are nicely calibrated. It combines calibration and discrimination.

Learn extra: Calibration of Machine Studying Fashions

Case Examine utilizing PyTorch

Right here, we’ll use the BigMart Gross sales dataset to display how the customized loss features and the calibration matrices assist in predicting the goal column, OutletSales.

We modify the continual OutletSales to a binary Excessive vs Low class by thresholding on the median. We then match a easy classifier in PyTorch utilizing options resembling product visibility, after which apply customized loss and calibration. 

Key steps

Knowledge Preparation and Preprocessing: On this half, we’ll import the libraries, load the information, and most significantly, do the information preprocessing steps. Like lacking worth dealing with, making the explicit column uniform (‘low fats’, ‘Low Fats’, and lf all are the identical so that they’ll develop into “Low Fats”), making a threshold for the goal variable, performing OHE (One-hot encoding) on categorical variables, and splitting the options.

import os
import random
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt

import torch
import torch.nn as nn
import torch.nn.practical as F
from torch.utils.information import TensorDataset, DataLoader, random_split

from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import classification_report, confusion_matrix
from sklearn.utils.class_weight import compute_class_weight


SEED = 42
random.seed(SEED)
np.random.seed(SEED)
torch.manual_seed(SEED)

if torch.cuda.is_available():
    torch.cuda.manual_seed_all(SEED)

system = torch.system('cuda' if torch.cuda.is_available() else 'cpu')
print('Machine:', system)

# ----- missing-value dealing with -----
df['Weight'].fillna(df['Weight'].imply(), inplace=True)
df['OutletSize'].fillna(df['OutletSize'].mode()[0], inplace=True)

# ----- categorical cleansing -----
df['FatContent'].substitute(
    {'low fats': 'Low Fats', 'LF': 'Low Fats', 'reg': 'Common'},
    inplace=True
)

# ----- classification goal -----
threshold = df['OutletSales'].median()
df['SalesCategory'] = (df['OutletSales'] > threshold).astype(int)

# ----- one-hot encode categoricals -----
cat_cols = [
    'FatContent', 'ProductType', 'OutletID',
    'OutletSize', 'LocationType', 'OutletType'
]
df = pd.get_dummies(df, columns=cat_cols, drop_first=True)

# ----- cut up options / labels -----
X = df.drop(['ProductID', 'OutletSales', 'SalesCategory'], axis=1).values
y = df['SalesCategory'].values

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.2, random_state=SEED, stratify=y
)

scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.rework(X_test)

# create torch tensors
X_train_t = torch.tensor(X_train, dtype=torch.float32)
y_train_t = torch.tensor(y_train, dtype=torch.lengthy)
X_test_t = torch.tensor(X_test, dtype=torch.float32)
y_test_t = torch.tensor(y_test, dtype=torch.lengthy)

# cut up practice into practice/val (80/20 of authentic practice)
val_frac = 0.2
val_size = int(len(X_train_t) * val_frac)
train_size = len(X_train_t) - val_size

train_ds, val_ds = random_split(
    TensorDataset(X_train_t, y_train_t),
    [train_size, val_size],
    generator=torch.Generator().manual_seed(SEED)
)

train_loader = DataLoader(
    train_ds, batch_size=64, shuffle=True, drop_last=True
)
val_loader = DataLoader(
    val_ds, batch_size=256, shuffle=False
)

Customized Loss: Within the 2nd step, first, we’ll create a customized SalesClassifier. Take into account that we apply Focal Loss to put extra emphasis on the minority class. Then, we’ll refit the mannequin to maximise Focal Loss as a substitute of Cross Entropy Loss. In lots of circumstances, the Focal Loss will increase recall on the minor class however might lower uncooked accuracy. After that, we’ll practice our gross sales classifier with the assistance of the customized SoftF1Loss over 100 epochs and save the perfect mannequin as best_model.pt

class SalesClassifier(nn.Module):

   def __init__(self, input_dim):

       tremendous().__init__()

       self.internet = nn.Sequential(

           nn.Linear(input_dim, 128),

           nn.BatchNorm1d(128),

           nn.ReLU(inplace=True),

           nn.Dropout(0.5),

           nn.Linear(128, 64),

           nn.ReLU(inplace=True),

           nn.Dropout(0.25),

           nn.Linear(64, 2)          # logits for two lessons

       )

   def ahead(self, x):

       return self.internet(x)

# class-weighted CrossEntropy to battle imbalance

class_weights = compute_class_weight('balanced',

                                    lessons=np.distinctive(y_train),

                                    y=y_train)

class_weights = torch.tensor(class_weights, dtype=torch.float32,

                            system=system)

ce_loss = nn.CrossEntropyLoss(weight=class_weights)

Right here, we’ll be utilizing a customized loss perform named SoftF1Loss. So right here the SoftF1Loss is a customized loss perform that straight optimizes for the F1-score in a differentiable approach, making it appropriate for gradient-based coaching. As a substitute of utilizing arduous 0/1 predictions, it really works with smooth possibilities from the mannequin’s output (torch.softmax), so the loss modifications easily as predictions change. It calculates the smooth true positives (TP), false positives (FP), and false negatives (FN) utilizing these possibilities and the true labels, then computes smooth precision and recall. From these, it derives a “smooth” F1-score and returns 1 – F1 in order that minimizing the loss will maximize the F1-score. That is particularly helpful when coping with imbalanced datasets the place accuracy isn’t measure of efficiency.

# Differentiable Customized Loss Operate Tender-F1 loss

class SoftF1Loss(nn.Module):

   def ahead(self, logits, labels):

       probs = torch.softmax(logits, dim=1)[:, 1]   # positive-class prob

       labels = labels.float()

       tp = (probs * labels).sum()

       fp = (probs * (1 - labels)).sum()

       fn = ((1 - probs) * labels).sum()

       precision = tp / (tp + fp + 1e-7)

       recall    = tp / (tp + fn + 1e-7)

       f1 = 2 * precision * recall / (precision + recall + 1e-7)

       return 1 - f1

f1_loss = SoftF1Loss()

def total_loss(logits, targets, alpha=0.5):

   return alpha * ce_loss(logits, targets) + (1 - alpha) * f1_loss(logits, targets)

mannequin = SalesClassifier(X_train.form[1]).to(system)

optimizer = torch.optim.Adam(mannequin.parameters(), lr=1e-3)

best_val = float('inf'); persistence=10; patience_cnt=0

for epoch in vary(1, 101):

   mannequin.practice()

   train_losses = []

   for xb, yb in train_loader:

       xb, yb = xb.to(system), yb.to(system)

       optimizer.zero_grad()

       logits = mannequin(xb)

       loss = total_loss(logits, yb)

       loss.backward()

       optimizer.step()

       train_losses.append(loss.merchandise())

   # ----- validation -----

   mannequin.eval()

   with torch.no_grad():

       val_losses = []

       for xb, yb in val_loader:

           xb, yb = xb.to(system), yb.to(system)

           val_losses.append(total_loss(mannequin(xb), yb).merchandise())

       val_loss = np.imply(val_losses)

   if epoch % 10 == 0:

       print(f'Epoch {epoch:3d} | TrainLoss {np.imply(train_losses):.4f}'

             f' | ValLoss {val_loss:.4f}')

   # ----- early stopping -----

   if val_loss = persistence:

           print('Early stopping!')

           break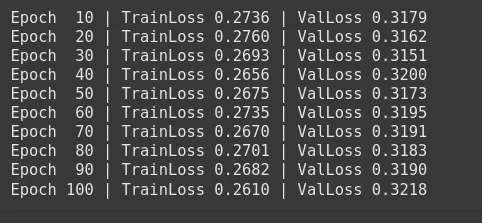

# load finest weights

mannequin.load_state_dict(torch.load('best_model.pt'))

Calibration Earlier than/After: On this circulation, we might have discovered that the ECE for the baseline mannequin was excessive, indicating the mannequin was overconfident. So the  Anticipated Calibration Error (ECE) for the baseline mannequin could also be excessive/low, indicating the mannequin was overconfident/underconfident. 

We are able to now calibrate the mannequin utilizing temperature scaling after which repeat the method to calculate a brand new ECE and plot a brand new reliability curve. We are going to see that the reliability curve might transfer nearer to the diagonal after temperature scaling happens.

class ModelWithTemperature(nn.Module):

   def __init__(self, mannequin):

       tremendous().__init__()

       self.mannequin = mannequin

       self.temperature = nn.Parameter(torch.ones(1) * 1.5)

   def ahead(self, x):

       logits = self.mannequin(x)

       return logits / self.temperature

model_ts = ModelWithTemperature(mannequin).to(system)

optim_ts = torch.optim.LBFGS([model_ts.temperature], lr=0.01, max_iter=50)

def _nll():

   optim_ts.zero_grad()

   logits = model_ts(X_val := X_test_t.to(system))   # use check set to suit T

   loss = ce_loss(logits, y_test_t.to(system))

   loss.backward()

   return loss

optim_ts.step(_nll)

print('Optimum temperature:', model_ts.temperature.merchandise())

Optimum temperature: 1.585491418838501

Visualization: On this part, we’ll be plotting reliability diagrams “earlier than” and “after” calibration. The diagrams are a visible illustration of the improved alignment.

@torch.no_grad()

def get_probs(mdl, X):

   mdl.eval()

   logits = mdl(X.to(system))

   return F.softmax(logits, dim=1).cpu()

def ece(probs, labels, n_bins=10):

   conf, preds = probs.max(1)

   accs = preds.eq(labels)

   bins = torch.linspace(0,1,n_bins+1)

   ece_val = torch.zeros(1)

   for lo, hello in zip(bins[:-1], bins[1:]):

       masks = (conf>lo) & (confbins[i]) & (conf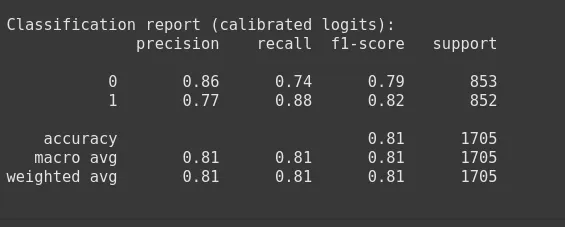

print('ECE earlier than T-scaling :', ece(probs_before, y_test_t))

print('ECE after  T-scaling :', ece(probs_after , y_test_t))

#----------------------------------------

# ECE earlier than T-scaling : 0.05823298543691635

# ECE after  T-scaling : 0.02461853437125683

# ----------------------------------------------

# reliability plot

fig, ax = plt.subplots(figsize=(6,5))

plot_reliability(ax, probs_before, y_test_t, label="Earlier than T-Scaling")

plot_reliability(ax, probs_after , y_test_t, label="After  T-Scaling")

plt.present()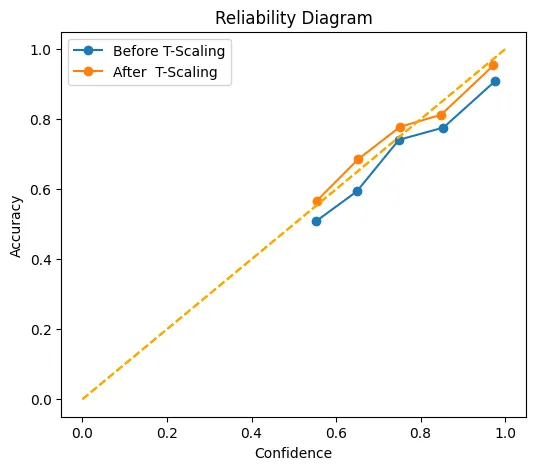

This chart exhibits how nicely the boldness rating matches/aligns with the precise values, each earlier than (blue) and after (orange) temperature scaling. The x-axis displays their imply acknowledged confidence, whereas the y-axis displays how often these predictions have been scored correctly. The dotted diagonal line represents excellent calibration factors that coincide with this line, representing.

For instance, predictions which are scored with 70% confidence are accurately scored 70% of the time. After scaling, the orange line hugs this diagonal line extra intently than the blue line does. Particularly within the ‘center’ of the boldness area between 0.6 and 0.9 confidence, and nearly meets the perfect level at (1.0, 1.0). In different phrases, temperature scaling has the potential to scale back the mannequin’s proclivity towards over- or under-confidence in order that its level estimates of the chance are significantly extra correct.

Test the entire pocket book right here.

Conclusion

In real-world AI functions, validity and calibration are equally essential. A mannequin might have excessive validity, but when the mannequin’s confidence isn’t correct, then there’s little worth in having greater validity. Due to this fact, growing customized loss features specific to your downside assertion throughout the coaching can match our true goals, and we consider calibration so we are able to interpret predictive possibilities appropriately. 

Due to this fact full analysis technique considers each: we first permit the customized losses to totally optimize the mannequin for the duty, after which we deliberately calibrate and validate the chance outputs. Now we are able to create a decision-support software, the place a “90% confidence” actually is “90% possible,” which is crucial for any real-world implementation.

Learn extra: High 7 Loss features for Regression fashions

Often Requested Questions

Good day! I am Vipin, a passionate information science and machine studying fanatic with a powerful basis in information evaluation, machine studying algorithms, and programming. I’ve hands-on expertise in constructing fashions, managing messy information, and fixing real-world issues. My purpose is to use data-driven insights to create sensible options that drive outcomes. I am wanting to contribute my abilities in a collaborative atmosphere whereas persevering with to be taught and develop within the fields of Knowledge Science, Machine Studying, and NLP.